"Pour apprendre et pour comprendre, on a besoin d'images mentales, d'évocations visuelles et auditives" explique Antoine de la Garanderie dans son ouvrage "les profils pédagogiques".
Dans un échange avec un adulte non pédagogue, Brigitte Toulemonde, enseignante à la retraite, souligne l'importance de ces profils pour la compréhension et l'apprentissage. Elle prend l'exemple d'un théorème mathématiques qu'elle ne maitrise pas. En se plaçant dans la situation d'un élève qui n'a pas bien compris sa leçon, elle montre les écueils qui peuvent apparaître lors du cheminement du processus de compréhension et de mémorisation.
L'exemple du théorème de Pythagore
Brigitte : le théorème de Pythagore, c’est quoi pour toi ? (c’est le premier exemple qui me passe par la tête , j’ai toujours trouvé ce nom de Pythagore très amusant au milieu du livre de maths peu attrayant !)
Thierry : A²= B²+C²
Brigitte : Oui, je me souviens de cette formule (que je me redis dans ma tête). Mais je suis incapable de la mettre dans un contexte, de savoir à quoi elle peut me servir, je n’en ai que le souvenir auditif.
Thierry : cela peut aussi se dire : A*A= B*B + C*C
Brigitte écrit consciencieusement ce que lui dit Thierry. Mais, pour elle, c’est toujours le trou noir quand à l’utilisation de cette formule.
Thierry : Le carré de l’hypoténuse égale la somme du carré de chaque côté d’un triangle rectangle.
La formule se développe en mots, cela devrait aider Brigitte. Elle sait, grâce au mot « triangle » qu'ils sont entrés dans le domaine de la géométrie. Mais elle ne sait plus ce qu’est une hypoténuse.
| Alors Thierry prend mon papier et dessine |
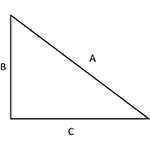 |
Brgitte : Pour toi, tout cela semble si simple, pour moi, c’est encore le brouillard : où se situe l’hypoténuse ? Je crois que je la confonds avec la hauteur. Peux-tu me « dire » comment je dois procéder.
Thierry : Tu traces un angle droit avec 2 côtés B et C. Tu traces l’hypoténuse à partir de l’extrémité de B et de l’extrémité de C. Tu l’appelles A.
La longueur de l’hypoténuse A se calcule de la manière suivante : A²= B²+C² ou, autrement dit : A = racine carré de B²+C².
Brigitte s’exécute au fur et à mesure des consignes tout en se les redisant dans sa tête (je …, je…)
Brigitte conclue : nous avons continué ainsi le développement puis avec des exemples et chaque fois pour moi la nécessité de formuler avec des mots (et dans un discours) ce qui pour Thierry passait par une formule ou un croquis.